삽입 정렬에 대해 알아보자.
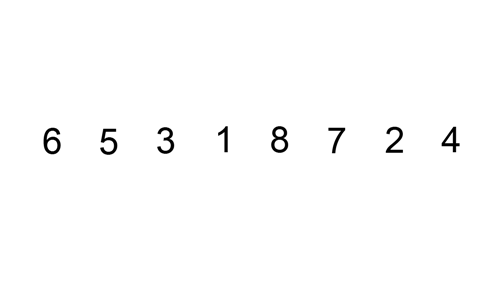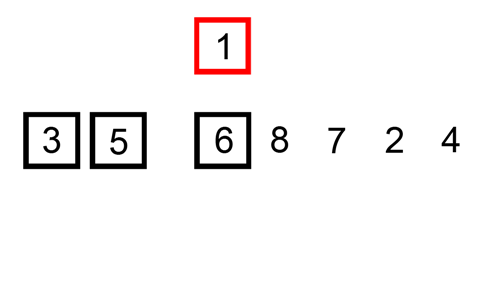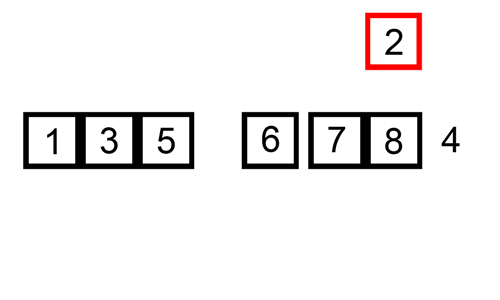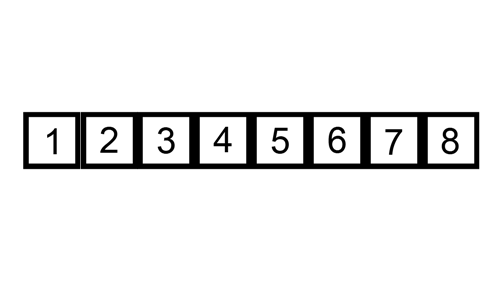
개념
정렬되지 않은 임의의 데이터를 이미 정렬된 부분의 적절한 위치에 삽입해 가며 정렬한다.
특징
버블/선택 정렬은 내부에서 정렬이 거듭될수록 탐색 범위가 줄어든다.
하지만 삽입 정렬은 오히려 정렬 범위가 늘어난다.
복잡도
버블, 선택 정렬과 마찬가지로 별도의 추가 공간을 사용하지 않는다.
주어진 배열 내에서 값들이 위치를 변경하기 때문에 공간 복잡도는 O(1)이다.
모든 데이터가 현재 데이터가 되어야 하므로 O(N)이 필요하다.
현재 데이터는 정렬된 데이터들과 비교하기 위해 O(N)이 필요하다. 따라서 시간복잡도는 O(N^2)이다.
구현
def insertion_sort(li):
for end in range(1, len(li)):
for i in range(end, 0, -1):
if li[i - 1] > li[i]:
li[i - 1], li[i] = li[i], li[i - 1]
최적화 1
정렬된 부분에서 현재 데이터보다 작은 값이 나오면, 현재 데이터와 작은 값 앞에 데이터들은 비교할 필요가 없다.
따라서 break로 더 이상 비교하지 않는다.
def insertion_sort(li):
for end in range(1, len(li)):
for i in range(end, 0, -1):
if li[i - 1] > li[i]:
li[i - 1], li[i] = li[i], li[i - 1]
else:
break
예를 들어, [1, 2, 4, 3]이 있다.
0. [1, 2, 4, 3] : 현재 데이터는 1
1. [1, 2, 4, 3] : 현재 데이터는 2
2. [1, 2, 4, 3] : 현재 데이터는 4
3. [1, 2, 3, 4] : 현재 데이터는 3
2번을 보자. 4는 바로 앞에 있는 2보다 더 큰 값이다.
따라서 2 앞에 있는 1과는 비교할 필요도 없다.
이렇게 최적화 했을 때, 이미 정렬된 배열이 들어오면 시간 복잡도가 O(N)이다.
최적화 2
정렬된 배열에서 현재 데이터보다 큰 값이 나올 때마다 자리를 교대[swap]했다.이번에는 swap말고, shift로 구현해보자.
def insertion_sort(li):
for end in range(1, len(li)):
to_insert = li[end] # 현재 데이터
i = end
while i > 0 and li[i - 1] > to_insert:
li[i] = li[i - 1] # shift
i -= 1
li[i] = to_insert # 현재 데이터를 적절한 위치에 삽입
예를 들어, [1, 2, 4, 5, 3]이 있다.
현재 데이터가 3이라고 하자.
[1, 2, 4, 5, 3]
[1, 2, 4, 5, 5]
[1, 2, 4, 4, 5]
[1, 2, 3, 4, 5]
이렇게 동작한다.
현재 데이터를 저장해놨다가, 현재 데이터보다 최초로 작은 값 뒤에 삽입한다.
현재 데이터보다 큰 값은 Shift를 한다.
'알고리즘 > 개념' 카테고리의 다른 글
| [이진탐색] 하한선[Lower bound], 상한선[Upper bound] (0) | 2022.03.03 |
|---|---|
| [정렬] 각 정렬의 장단점 및 시간 복잡도 (0) | 2022.02.10 |
| [정렬] 선택 정렬 [Selection Sort] (0) | 2022.02.09 |
| [정렬] 버블 정렬 [Bubble Sort] (0) | 2022.02.08 |
| [시간 복잡도] 빅오 표기법[Big O notation] (0) | 2022.01.05 |



