[그래프/트리] 분리 집합[Disjoint Set]

분리 집합은 서로소 집합이다. (상호 배타적 집합)

 

Union-Find 알고리즘을 사용하고, 트리 구조를 이용해 구현한다.

 

참고로,

트리 구조는 부모노드가 자식 노드를 가리키는 형태이지만,

분리 집합은 자식 노드가 부모노드를 가리키는 형태이다.

 

 

Union-Find

 

Union-Find는 서로소 집합 알고리즘이다.

 

여러 개의 노드가 존재할 때 두 개의 노드를 선택해서,

현재 이 두 노드가 서로 같은 집합에 속하는지 판별하는 알고리즘이다.

 

 

Union-Find는 두 가지 수행이 필요하다.

 

Find

노드 x가 어느 집합에 포함되어 있는지 찾는다.

 

Union

노드 x가 포함된 집합과 노드 y가 포함된 집합을 합친다.

 

 

Union-Find 구현

 

 

초기화

 

 

parent = [i for i in range(0, n + 1)]

 

 

i 노드의 부모노드는 parent[i]라고 정의하고 초기화 한다.(parent[i]의 값이 i라면, 루트 노드이다.)

 

 

 

Find

 

 

def find(x):
    if x == parent[x]:
        return x
    
    else:
        return find(parent[x])

 

 

재귀함수를 사용하여 루트 노드를 찾는다.

 

하지만 위와 같이 구현할 경우,

아래 그림처럼 tree가 한쪽으로 치우쳐진다. 

루트 노드를 찾는데 O(N)이 되고 tree 구현의 이점이 사라진다.

 

 

https://ssungkang.tistory.com/entry/Algorithm-%EC%9C%A0%EB%8B%88%EC%98%A8-%ED%8C%8C%EC%9D%B8%EB%93%9CUnion-Find

 

 

해결해보자.

 

 

def find(x):
    if x == parent[x]:
        return x
    
    else:
        y = find(parent[x])
        parent[x] = y
        
        return y

 

 

아래 그림처럼, 부모를 루트 노드로 바꾸어준다.

 

 

https://ssungkang.tistory.com/entry/Algorithm-%EC%9C%A0%EB%8B%88%EC%98%A8-%ED%8C%8C%EC%9D%B8%EB%93%9CUnion-Find

 

 

 

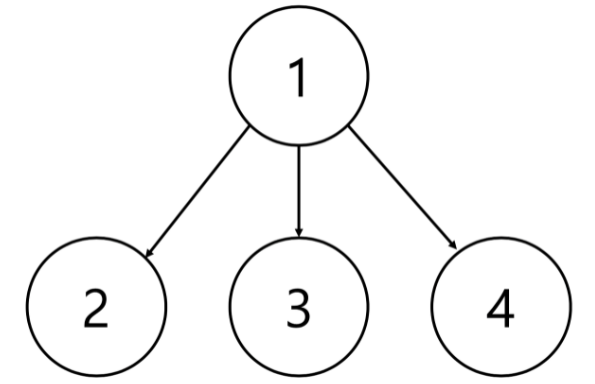
Union

 

 

def union(x, y):
    x = find(x)
    y = find(y)

    if x == y:
        return

    if rank[x] < rank[y]:
    	a, b = y, x

    else:
    	a, b = x, y

    if rank[x] == rank[y]:
    	rank[b] += 1
    
    parent[a] = b

 

 

부모를 합칠 때는 일반적으로 더 작은 값 쪽으로 합친다. (문제에서 조건을 준다.)

 

그리고 고려해야 할 점은 트리의 높이이다.

 

(트리의 높이 : 트리 중 가장 긴 경로의 간선 개수

트리의 깊이 : 루트에서 현재 노드 사이의 간선 개수

트리의 레벨 : 트리 중 깊은 노드의 개수)

 

 

https://gsmesie692.tistory.com/227

 

 

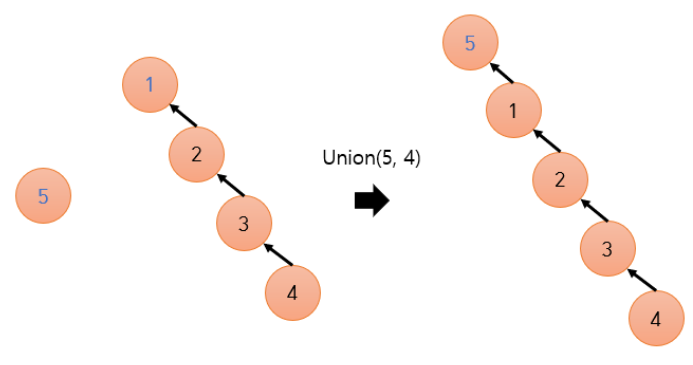
예를 들어, A는 높이가 0이고 B는 높이가 4이다.

A가 B로 합쳐질 때 문제가 안 되지만,

위 그림처럼, B가 A로 합쳐질 때 문제가 된다.

(높이가, 낮은 트리 밑에 높은 트리를 넣으면 문제가 된다.)

 

높이가 계속 높아지는 편향 트리가 되기 때문이다.

따라서 Find 수행 시, 루트 노드를 찾는데 더 오랜 시간이 걸리게 된다.

 

트리의 장점 중 하나는 빠른 탐색 속도이다.

완전 이진 탐색 트리의 경우 바닥에서 루트까지 타고 올라가는데 걸리는 평균 시간 복잡도는 O(logN)이다.

하지만 저렇게 높이가 길어지면, 선형 리스트를 쓰는 것과 다름없는 O(N)만큼의 시간이 걸린다.

 

 

트리의 높이의 초깃값을 할당하고, 증가시켜야한다.

 

트리의 높이의 초깃값은 1이다.

 

트리의 높이는 언제 증가하는지 생각해보자.

트리의 높이는 합쳐진, 두 트리의 높이가 같을 때만 증가하게 된다.

 

예를 들어, 높이가 h인 트리를 만들기 위해서는 높이가 h-1인 트리 2개를 합쳐야 한다. 

 

 

왜 시간 복잡도가 O(logN)인지 확인해보자.

 

높이가 h-1이 되기 위해서 최소 x개의 노드가 필요하다면, 높이가 h가 되기 위해서는 최소 2x의 노드가 필요하다.

[트리의 높이]가 [포함한 노드의 수의 로그]에 비례하는 것을 보장하게 되므로

위에서 최적화한 Union-Find의 시간 복잡도가 O(logN)인 것을 확인할 수 있다.