병합 또는 합병 정렬에 대해 알아보자.
이는 분할 정복 방법을 통해 구현한다.
(분할 정복은 큰 문제를 작은 문제 단위로 쪼개면서, 쉽게 풀 수 있는 문제 단위로 나눈 뒤 그것들을 다시 합치는 방식이다.)
퀵 정렬과 함께 빠른 정렬에 해당한다.
예를 들어보자.
[6, 5, 3, 1, 8, 7, 2, 4]
숫자 1 ~ 8까지 들어있는 배열이 있다.
먼저 하나의 배열을 두 개로 쪼갠다.
[6, 5, 3, 1] [8, 7, 2, 4]
그리고 다시 각 배열을 두 개로 쪼갠다.
[6, 5] [3, 1] [8, 7] [2, 4]
또다시 각 배열을 두 개로 쪼갠다.
[6] [5] [3] [1] [8] [7] [2] [4]
이제 더 이상 배열을 쪼갤 수 없다. 이제 두 개의 배열씩 합친다.
합칠 때는 둘 중에 값이 더 작은 배열을 앞에 위치시킨다.
[5, 6] [1, 3] [7, 8] [2, 4]
또 두 개의 배열씩 합친다.
합칠 때는
1. 각 배열에서 가장 작은 원소끼리 비교한다.
2. 둘 중 더 작은 원소를 선택한다. 선택된 원소는 다음 비교에서 제외한다.
3. 모든 원소가 선택될 때까지 1, 2번을 반복한다.
[1, 3, 5, 6] [2, 4, 7, 8]
마찬가지로 두 개의 배열을 합친다.
[1, 2, 3, 4, 5, 6, 7, 8]
최종적으로 정렬된 형태를 볼 수 있다.
이 알고리즘은 분할(split)단계와 병합(merge)단계로 나뉜다.
분할단계는 8->4->2->1처럼 절반으로 계속 줄기 때문에 O(logN)이다.
병합단계는 병합할 때 모든 원소를 비교해야 해서 O(N)이다.
따라서 시간 복잡도는 O(NlogN)이다.
분할 정복의 개념을 다시 보고, 구현해보자.
큰 문제를 작은 문제 단위로 쪼개면서 => 분할(split)
쉽게 풀 수 있는 문제 단위로 나눈 뒤 => 배열을 더 이상 나눌 수 없을 때까지
그것들을 다시 합치는 방식이다. => 병합(merge)
def merge_sort(li):
length = len(li)
# 더 이상 나눌 수 없는가?
if length == 1:
return li
# 분할
mid = length // 2
front_li = merge_sort(li[:mid])
back_li = merge_sort(li[mid:])
print("f:", front_li, "b:", back_li, mid)
# 병합
merged_li = []
i = j = 0
while i < len(front_li) and j < len(back_li):
if front_li[i] < back_li[j]:
merged_li.append(front_li[i])
i += 1
else:
merged_li.append(back_li[j])
j += 1
merged_li += front_li[i:]
merged_li += back_li[j:]
print("병합:", merged_li)
print()
return merged_li
merge_sort([5, 6, 1, 3, 7, 8, 2, 4])
아래는 실행 결과이다.
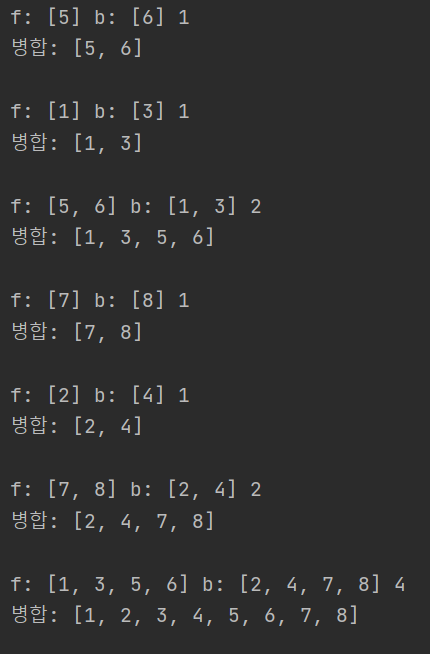
앞부분만 설명해보면 아래와 같다.
[5]와 [6]이 병합되어 [5, 6]이 되었고, 이는 다시 front_li가 된다.
[1]과 [3]이 병합되어 [1, 3]이 되었고, 이는 다시 back_li가 된다.
그리고 [5, 6]과 [1, 3]이 병합되어 [1, 3, 5, 6]이 되고 이는 다시 front_li가 된다.
위처럼 구현해도 되지만, 리스트 슬라이싱으로 배열을 복제했기 때문에 메모리 사용 효율이 높지 않다.
매번 새로운 배열을 리턴하지 말고, 인덱스 접근으로 배열을 매번 업데이트 해보자. [In-place sort]
def merge_sort(li):
def sort(low, high):
# 더 이상 나눌 수 없는가?
if high - low < 2:
return
mid = (low + high) // 2
sort(low, mid) # front
sort(mid, high) # back
merge(low, mid, high) # 병합
print(li)
def merge(front, mid, back):
temp = []
i, j = front, mid
while i < mid and j < back:
if li[i] < li[j]:
temp.append(li[i])
i += 1
else:
temp.append(li[j])
j += 1
while i < mid:
temp.append(li[i])
i += 1
while j < back:
temp.append(li[j])
j += 1
for k in range(front, back):
li[k] = temp[k - front]
return sort(0, len(li))
merge_sort([5, 6, 1, 3, 7, 8, 2, 4])
저장을 안 해서 글이 한번 날아갔다. 정말 슬펐다....🥺
'알고리즘 > 개념' 카테고리의 다른 글
| [정렬] stable vs not stable (0) | 2021.12.03 |
|---|---|
| [정렬] 퀵 정렬 [Quick Sort] (0) | 2021.12.03 |
| [최소 신장 트리] 프림[Prim] 알고리즘 (0) | 2021.10.08 |
| [정렬] 위상 정렬(Topological Sort) (0) | 2021.10.02 |
| [최단 경로 트리] 다익스트라 알고리즘[Dijkstra] (0) | 2021.05.18 |



