퀵 정렬에 대해 알아보자.
이는 분할 정복을 통해 구현한다.
(분할 정복은 큰 문제를 작은 문제 단위로 쪼개면서, 쉽게 풀 수 있는 문제 단위로 나눈 뒤 그것들을 다시 합치는 방식이다.)
불안정 정렬이고 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬이다.
그리고 병합 정렬과 함께 빠른 정렬에 해당한다.
병합 정렬과는 분할 정복을 통해 해결한다는 공통점이 있다.
차이점은 아래와 같다.
1) 병합 정렬 : O(n)의 시간이 걸리는 과정을 재귀호출 후에 한다.
(분할 후 병합 시점에서 비교 연산 발생)
2) 퀵 정렬 : O(n)의 시간이 걸리는 과정을 재귀호출 전에 한다.
(분할 시점부터 비교 연산 발생)
따라서 퀵 정렬이 병합에 들어가는 비용이 적거나
구현 방법에 따라서 아예 병합하지 않을 수도 있다.
퀵 정렬의 예를 들어보자.
[6, 5, 1, 4, 7, 2, 3]
숫자 1 ~ 7까지 들어있는 배열이 있다.
병합 정렬은 항상 배열의 중앙을 기준으로 분할한다. (균등 분할)
하지만 퀵 정렬은 pivot이라는 임의의 기준값을 기준으로 분할한다. (비균등 분할)
pivot 값을 선택하는 데는 여러 방법이 있다. 여기서는 중앙에 있는 값을 pivot으로 해보자.
그리고 pivot을 기준으로 왼쪽은 pivot보다 작은 값의 그룹, 오른쪽은 pivot보다 큰 값의 그룹으로 나눈다.
P
[1, 2, 3] < 4 < [6, 5, 7]
이런 식으로 분할을 하게 되면,
앞으로 (Pivot 값을 기준으로) 왼쪽 그룹과 오른쪽 그룹은 비교하지 않는다.
이제 왼쪽 그룹을 동일한 방식으로 정렬하자.
P
[1] < 2 < [3]
pivot을 기준으로 왼쪽은 pivot보다 작은 값의 그룹, 오른쪽은 pivot보다 큰 값의 그룹으로 나눈다.
P
[] < 5 < [6, 7]
이제 오른쪽 그룹을 동일한 방식으로 정렬하자.
pivot을 기준으로 왼쪽은 pivot보다 작은 값의 그룹, 오른쪽은 pivot보다 큰 값의 그룹으로 나눈다.
p
[6] < 7 < []
pivot을 기준으로 왼쪽은 pivot보다 작은 값의 그룹, 오른쪽은 pivot보다 큰 값의 그룹으로 나눈다.
[1, 2, 3, 4, 5, 6, 7]
그럼 이렇게 정렬된다.
이제 구현해보자.
def quick_sort(li):
if len(li) <= 1:
return li
pivot = li[len(li) // 2]
lesser_li, equal_li, greater_li = [], [], []
for num in li:
if num < pivot:
lesser_li.append(num)
elif num > pivot:
greater_li.append(num)
else:
equal_li.append(num)
return quick_sort(lesser_li) + equal_li + quick_sort(greater_li)
print(quick_sort([6, 5, 1, 4, 7, 2, 3]))
위처럼 구현하면,
계속 새로운 리스트를 생성하고 리턴하기 때문에 메모리 사용 측면에서 비효율적이다.
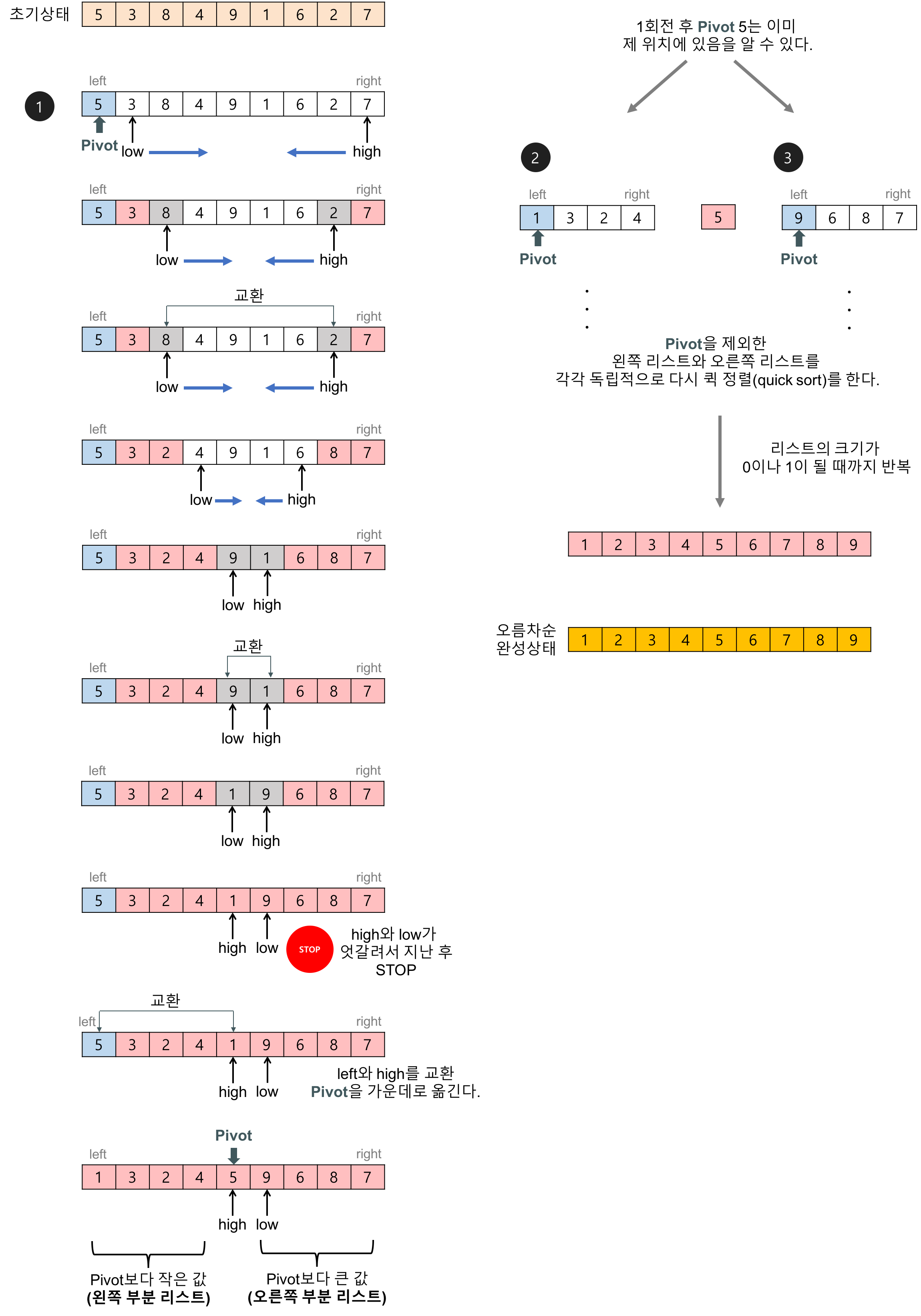
아래 이미지처럼 최적화 시키자.
def quick_sort(li):
def sort(low, high):
if high <= low:
return
mid = partition(low, high)
sort(low, mid - 1)
sort(mid, high)
def partition(low, high):
pivot = li[(low + high) // 2]
while low <= high:
while li[low] < pivot:
low += 1
while li[high] > pivot:
high -= 1
if low <= high:
li[low], li[high] = li[high], li[low]
low, high = low + 1, high - 1
return low
return sort(0, len(li) - 1)
print(quick_sort([6, 5, 1, 4, 7, 2, 3]))
평균 시간 복잡도는 O(nlogn)이다.
Pivot 값이 최소나 최댓값으로 지정돼서 분할이 잘 나누어지지 않으면
O(n^2)의 시간 복잡도를 가진다.
'알고리즘 > 개념' 카테고리의 다른 글
| [정렬] in-place vs not in-place (0) | 2021.12.03 |
|---|---|
| [정렬] stable vs not stable (0) | 2021.12.03 |
| [정렬] 병합 정렬 [Merge Sort] (0) | 2021.12.01 |
| [최소 신장 트리] 프림[Prim] 알고리즘 (0) | 2021.10.08 |
| [정렬] 위상 정렬(Topological Sort) (0) | 2021.10.02 |


