[최단 경로 트리] 플로이드-워셜 알고리즘[Floyd-Warshall]

플로이드-워셜 알고리즘에 대해 알아보자.

 

플로이드-워셜 알고리즘은 '거쳐 가는 기점'를 기준으로 최단 거리를 구한다.

예를 들어보자. 아래와 같은 그래프가 있다.

 

 

 

 

 

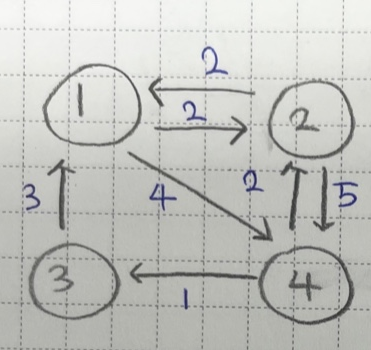
이차원 배열의 형태로 출력하면 다음과 같다.

 

 

 

 

위 상태의 테이블이 의미하는 바는 '현재까지 계산된 최소 비용'이다.

이제 이 배열을 '거쳐 가는 기점'을 기준으로 반복적으로 갱신할 것이다.

그렇게 한다면 결국엔 모든 A에서 B의 최소 비용을 구해진다.

 

 

---

 

거쳐 가는 기점이 1인 경우

 

 

 

 

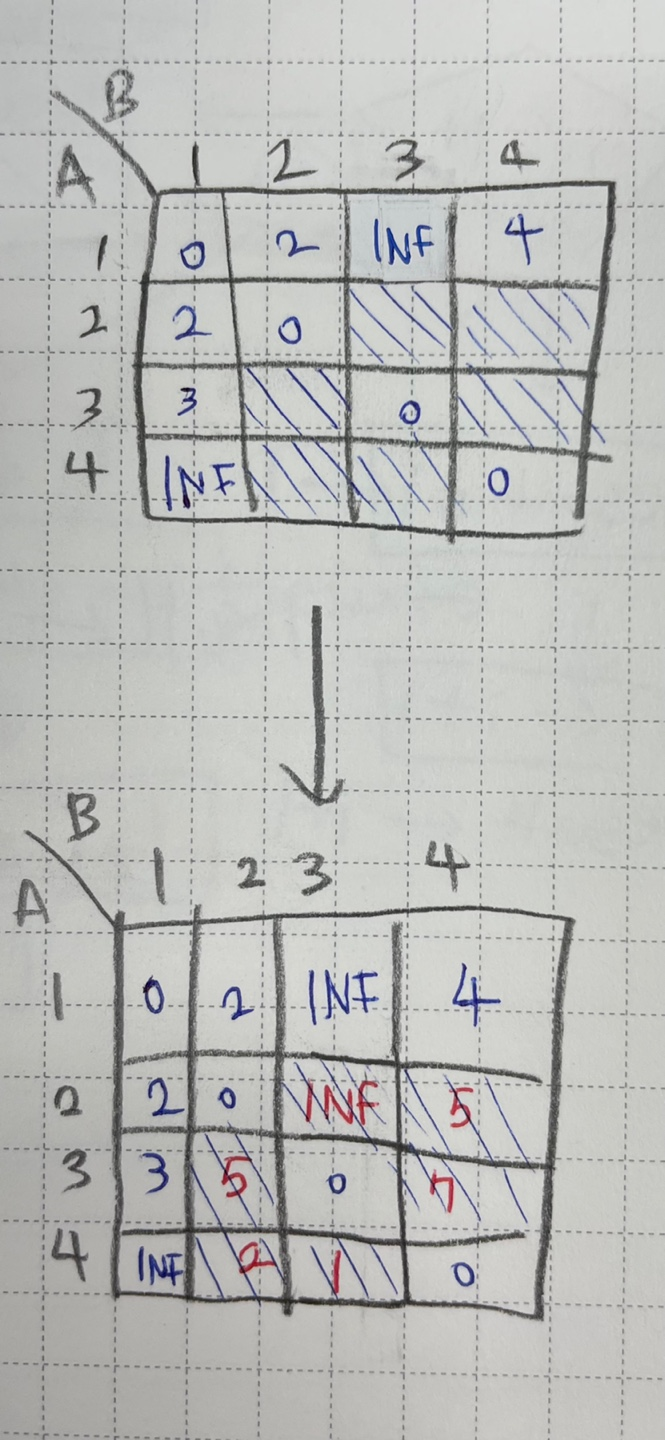
이렇게 거쳐 가는 기점이  1, 2, ... N인 경우를 모두 확인한다. 

 

 

---

 

다익스트라 알고리즘 vs 플로이드-워셜 알고리즘

 

공통점

거쳐 가는 노드를 기준으로 알고리즘을 수행한다.

 

차이점

다익스트라 알고리즘은 한 정점에서 다른 모든 정점으로의 최단 경로를 구한다.  

플로이드-워셜 알고리즘은 모든 정점에서 모든 정점으로의 최단 경로를 구한다.

 

 

---

 

아래 블로그를 참고하여 글을 작성했다.

https://blog.naver.com/ndb796/221234427842